Poison

Integer.bitCount

发表于

最近看 Richard Startin 关于 RoaringBitmap 的文章 A Quick Look at RoaringBitmap 时，提到 BitmapContainer 底层由 long[] 组成，内部使用了 Long.bitCount 计算容器的基数，此时会被优化为使用 CPU 指令 popcnt 实现，关于内联可以参考 JVM Intrinsics，本文先分析 bitCount 函数的实现机制，由于 Integer.bitCount 与 Long.bitCount 实现机制相同，就用 Integer.bitCount 进行分析。

首先从 Integer 的官方文档 Integer (Java Platform SE 8 ) 中，我们可以看到以下描述：

Implementation note: The implementations of the “bit twiddling” methods (such as highestOneBit and numberOfTrailingZeros) are based on material from Henry S. Warren, Jr.’s Hacker’s Delight, (Addison Wesley, 2002).

描述说明了 Integer 内部 bit 的相关方法实现来自于书籍 《Hacker’s Delight》，感兴趣的可以看看这本书籍。

先看 JDK 1.8 中 Integer.bitCount 的源码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * Returns the number of one-bits in the two's complement binary
 * representation of the specified {@code int} value.  This function is
 * sometimes referred to as the <i>population count</i>.
 *
 * @param i the value whose bits are to be counted
 * @return the number of one-bits in the two's complement binary
 *     representation of the specified {@code int} value.
 * @since 1.5
 */
public static int bitCount(int i) {
    // HD, Figure 5-2
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}

首次看到以上的实现时我不知所云，我们还是从书中的原始实现说起吧，假定一个有符号十进制数 -1134330113，其二进制表示为 0b10111100_01100011_01111110_11111111，如果我们需要统计二进制表示中 1 的个数，我们可以采取自底向上的分治算法实现，先以两个比特位为一个单元统计这两位中 1 的个数，容易看出这十六对以两个比特位组合中 1 的个数依次为：

1
1 2 2 0 1 1 0 2 1 2 2 1 2 2 2 2

我们再以 4 个比特位为一个单元进行统计，可以通过在两个比特位组合统计的基础上两两相加得到，即这 8 对 4 个比特位组合中 1 的个数为：

1
3 2 2 2 3 3 4 4

同理，再以 8 个比特位为一个单元进行统计，可以通过在 4 个比特位统计的基础上两两相加得到，即这 4 对 8 个比特位组合中 1 的个数为:

1
5 4 6 8

再以类似的方式，我们可以得到以 16 个比特位为一个单元时 1 的个数为:

1
9 14

最后得到以 32 个比特为一个单元时 1 的个数为:

1
23

以上实现为未经优化的 bitCount 的基础实现版本，我们现在将上面用到的中间值直接存储至 int 值的 bit 位上，如下图：


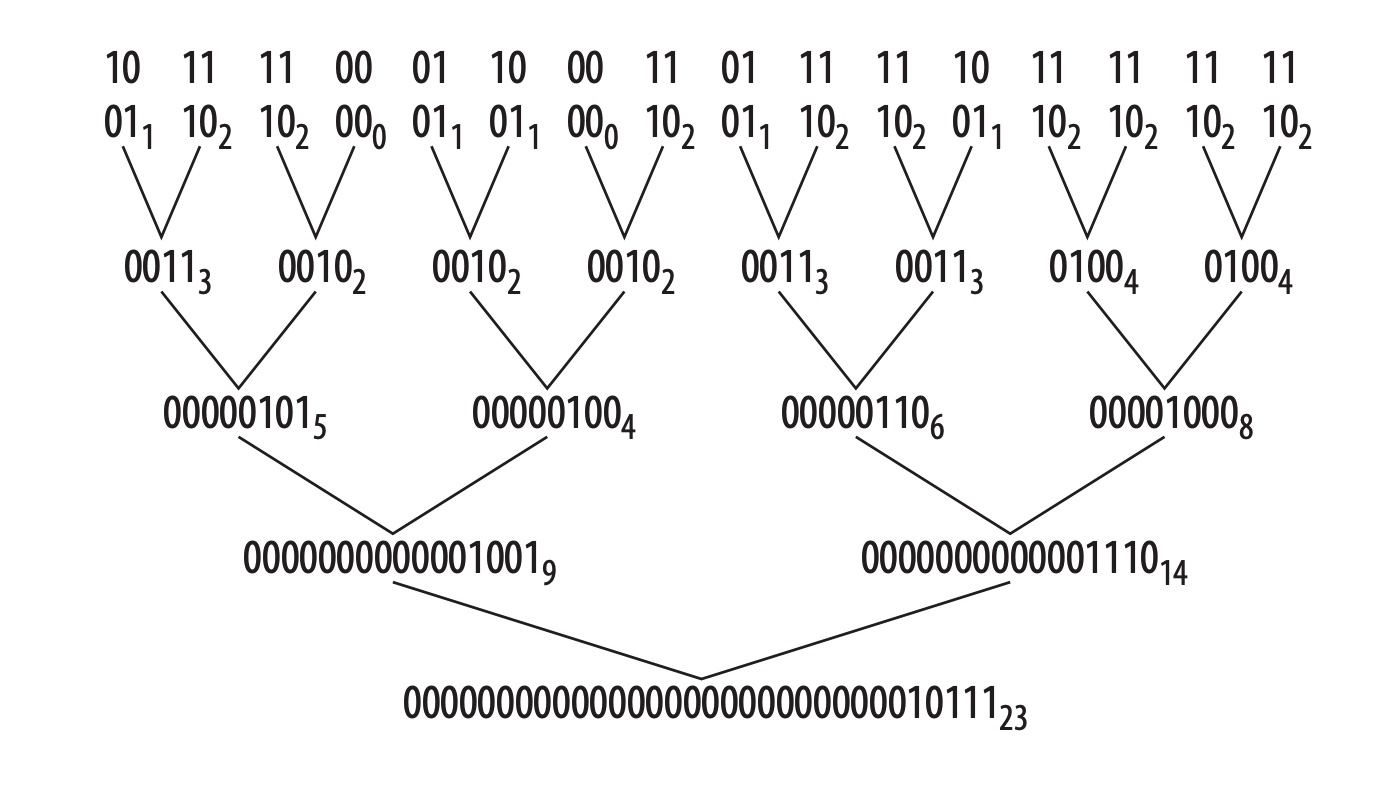
可以看出，我们之前用到的成对的 1 的个数以二进制的形式存储在 int 值的 bit 位上。以上的逻辑，通过代码的实现如下：

1
2
3
4
5
6
7
8
9
public static int bitCount(int i) {
    i = (i & 0b01010101_01010101_01010101_01010101) + ((i >>> 1) & 0b01010101_01010101_01010101_01010101); // line 1
    i = (i & 0b00110011_00110011_00110011_00110011) + ((i >>> 2) & 0b00110011_00110011_00110011_00110011); // line 2
    i = (i & 0b00001111_00001111_00001111_00001111) + ((i >>> 4) & 0b00001111_00001111_00001111_00001111); // line 3
    i = (i & 0b00000000_11111111_00000000_11111111) + ((i >>> 8) & 0b00000000_11111111_00000000_11111111); // line 4
    i = (i & 0b00000000_00000000_11111111_11111111) + ((i >>> 16) & 0b00000000_00000000_11111111_11111111); // line 5

    return i;
}

现在，我们在此实现的基础上进行优化，我们先看如下的计算：

1
2
3
4
0b00 = 0b00 - 0b00;
0b01 = 0b01 - 0b00;
0b01 = 0b10 - 0b01;
0b10 = 0b11 - 0b01;

等式左侧对应的十进制值表示为 1 的个数，右侧为 i - ((i >>> 1) & 0b01)，通过上面的算法即可以计算出 i 的二进制表示中 1 的个数并存储至二进制中，同样的方式，推广至 32 位二进制表示，我们可以将上面 bitCount 方法实现中的 line 1 优化为如下实现：

1
i = i - ((i >>> 1) & 0b01010101_01010101_01010101_01010101);

经过调整后，相比 line 1 的实现，减少了一次与运算。经过 line 2 的计算后，我们得到 4 个比特位为一个单元的组合，此时，即将进行的 line 3 将会把 4 个比特位的单位转换为 8 个比特位为一个单元，我们知道 8 个比特位全部为 1 时，十进制数 8 对应的二进制表示为 0b00001000，可知不会用到高 4 位，那么我们可以将 line 3 优化为如下实现：

1
i = (i + (i >>> 4)) & 0b00001111_00001111_00001111_00001111;

即先加每 4 个比特位的单元，再进行与计算，相比 line 3 的实现，减少了一次与运算。类似的原理，因为 int 的 32 个比特位全部为 1 时，十进制数 32 对应的二进制表示为 0b00100000，即用 6 个二进制位即可表示，所以我们可以将 line 4 和 line 5 优化为如下实现：

1
2
i = i + (i >>> 8);
i = i + (i >>> 16);

最后，因为移位产生的 6 位比特位左侧的 1，我们用一次与运算进行消除：

1
i = i & 0b00000000_00000000_00000000_00111111;

经过以上的优化，bitCount 的实现如下：

1
2
3
4
5
6
7
8
public static int bitCount(int i) {
    i = i - ((i >>> 1) & 0b01010101_01010101_01010101_01010101);
    i = (i & 0b00110011_00110011_00110011_00110011) + ((i >>> 2) & 0b00110011_00110011_00110011_00110011);
    i = (i + (i >>> 4)) & 0b00001111_00001111_00001111_00001111;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0b00000000_00000000_00000000_00111111;
}

最后，我们将易读的二进制表示调整为简短的十六进制表示，即为 JDK 中的 Integer.bitCount 实现：

1
2
3
4
5
6
7
8
public static int bitCount(int i) {
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}

以上仅是 bitCount 方法实现的一种，如果 i 的二进制只有很少的非零位，那么使用如下的算法效率更高：

1
2
3
4
5
6
7
8
9
public static int bitCount(int i) {
    int count = 0;
    while (i != 0) {
        i &= i - 1;
        count++;
    }

    return count;
}

其中 i &= i - 1; 会将二进制表示中最右侧的 1 转换为 0。如果允许更大的内存占用，那么我们还可以使用查表法，具体的可以参考：Hamming weight - Wikipedia。

Reference

5-1 Counting 1-Bits
代码之美
191. Number of 1 Bits
jdk/x86_64.ad at jdk8-b120 · openjdk/jdk · GitHub
Why do java intrinsic functions still have code? - Stack Overflow